“Por vezes e vezes ele dividiu, e mediu
espaço por espaço em sua nove vezes escuridão,
o não visto, o não conhecido, as mudanças apareceram
como montanhas desoladas, racharam furiosas
pelos ventos escuros da pertubação”
tradução livre do primeiro capitulo do livro de Urizen de William Blake

Em algum momento imaginei que eventualmente citaria William Blake. E em particular um de seus personagens de sua cosmogonia pessoal: Urizen. William Blake foi, se me permitem resumir seus feitos, um pintor e poeta inglês que viveu uma época de instabilidade religiosa na Inglaterra. Como os ingleses não seguiam os preceitos católicos vindos do Vaticano desde a rebelião de Henrique VIII o povo inglês era uma amalgama de vários grupos cristãos e cada grupo com a sua própria visão e valores do que era ser cristão.

Blake não era diferente dos demais ingleses. Tido por muitos como peculiar (talvez um eufemismo para o que alguns chamariam de loucura) ele afirmava que tinha visões e vislumbres de realidades mais sensíveis do que nós, indivíduos com menor capacidade visual/espiritual, apenas podemos conjecturar. Para nossa sorte Blake pintou e escreveu todas suas ideias e visões. E nesse processo criou sua própria cosmogonia e seu próprio panteão de personagens que prototipavam os arquétipos do ser humano, e por extensão, da realidade em sí.

Então voltamos ao homem da pintura acima. Ele é Urizen. Na cosmogonia de Blake é o lado racional do homem. Urizen, ou a razão, quando nasce e ve a sí própria, acredita que ela foi o motivo em sí mesma, e logo, não existe nada além dela. Então Urizen conclui que tudo ao seu redor deve nascer de sí.

Então caros amigos, criarmos um mundo tridimensional em um equipamento que usa apenas a lógica é onde exercemos a maior óde a Urizen possível. Aqui é onde estamos começando uma aventura em ideias de como simular a física de nosso mundo e até de compreender como a logica do próprio universo funciona para capturar essas ideias e representar em uma linguagem lógica que nossas maquinas de Turing consigam resolver e acender as cores certas na tela.

Do que você está falando ?

Neste texto nós vamos começar a representar figuras tridimensionais. Para isso vamos ter uma interpretação do espaço do mundo simulado e do espaço bidimensional da tela. E encontrar uma forma de identificar o que está na tela da câmera e, por fim, projetar o mundo tridimensional na tela. Estas ideias são a base da computação gráfica. E os algoritmos podem suscitar ideias sobre a simulação da realidade, o quão longe podemos ir e quais as restrições. Então vamos colorir nossas ideias e saber o que em nós esta assumindo o controle quando estamos no papel de criar um universo em nossas próprias mãos. Um spoiler: na cosmogonia de Blake, Urizen não necessariamente é o bonzinho da história.

Então como vai funcionar ? Bom nós queremos ter objetos com três dimensões em um espaço tridimensional e queremos ter alguma forma de filma-los, ou seja, alguma forma de saber quais objetos e/ou quais partes desses objetos estão na nossa tela. Então… vamos pensar em uma câmera. Imagine que teremos uma câmera onde o que ela captura na verdade vai ser nossa tela.

No post anterior nós chegamos na caneta de Urizen. Neste post vamos elaborar o esquadro e a régua.

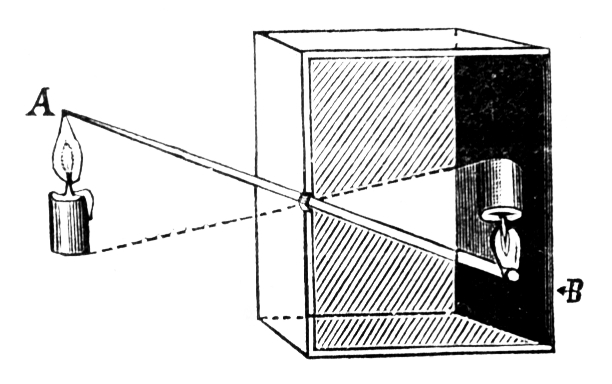
Uma câmera funciona como o experimento da câmara escura. Em que a fotografia ou o video é capturado dentro da câmera. Podemos reproduzir o experimento da câmera escura simplificado, onde o plano onde a luz vai ser projetada vai ser um plano conhecido, e esse plano vai ser a nossa tela.

A ideia para descobrir isso vai ser com um pouquinho de geometria. Mas o que queremos procurar é qual o ponto \(P'\) no plano de projeção para um ponto \(P\) no mundo. E vamos fazer essa pergunta para todos os pontos do mundo. Os pontos que estiverem dentro do intervalo da nossa tela \([-0.5, 0.5]\) em \(x\) e \([-0.5, 0.5]\) em \(y\). Dai com a nossa tela com vários pontos dos nossos polígonos tridimensionais, vai bastar fazer um mapeamento dos pontos tela->monitor que funcionaria como mapear \([-0.5, 0.5]=> [0, 1980] pixels\) para a largura e o mesmo para a altura. E com isso teremos o suficiente para projetar pontos tridimensionais para a nossa tela.

projetaObjetoTridimensional(objeto):
  para cada objeto no mundo:
    para cada ponto do objeto
      projete o ponto no plano

    desenhe linhas entre os pontos projetados

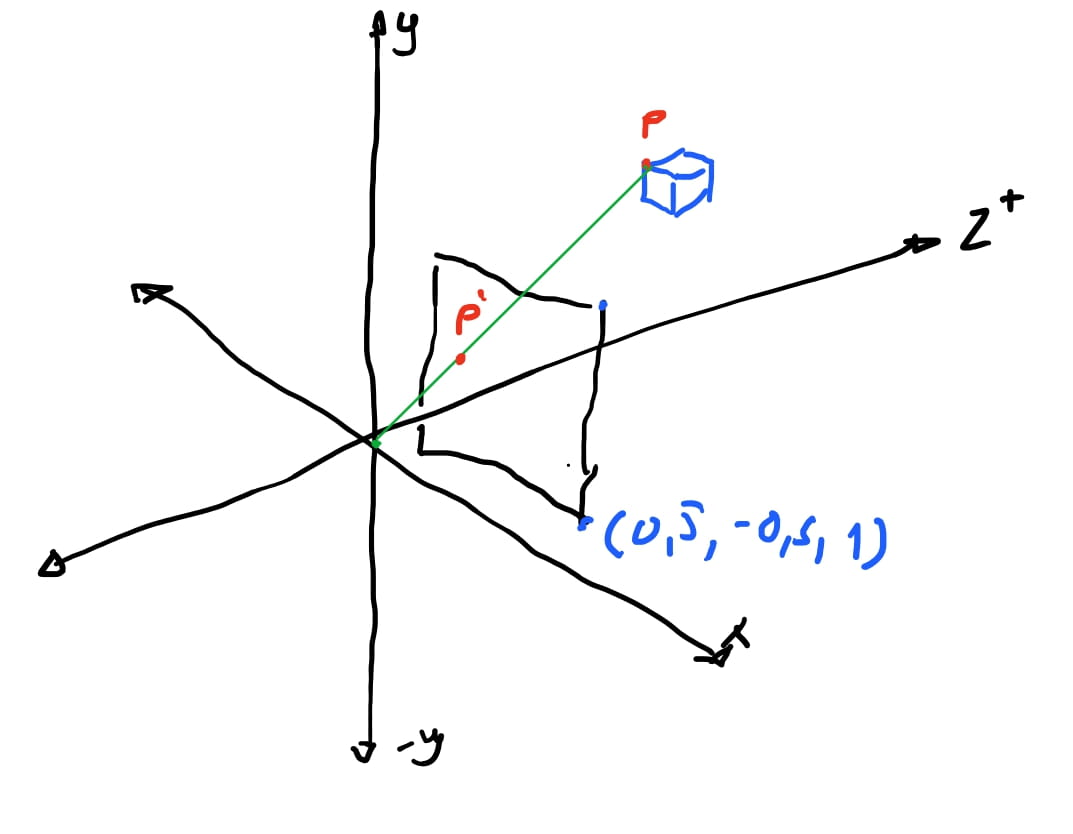Vamos usar a cena acima: temos um cubo na cena, e temos um plano centralizado em \(z_+\), e a uma distancia \(d = 1\).

Então vamos pensar como podemos obter \(P'\). Se olhar-mos a nossa cena de forma que o eixo \(y\) fique pra cima e o eixo \(z\) para a direita e o \(x\) na nossa direção, vemos que foma um triangulo com a reta que liga a origem \(O(0,0,0)\) cruzando o nosso plano de projeção \(proj\).

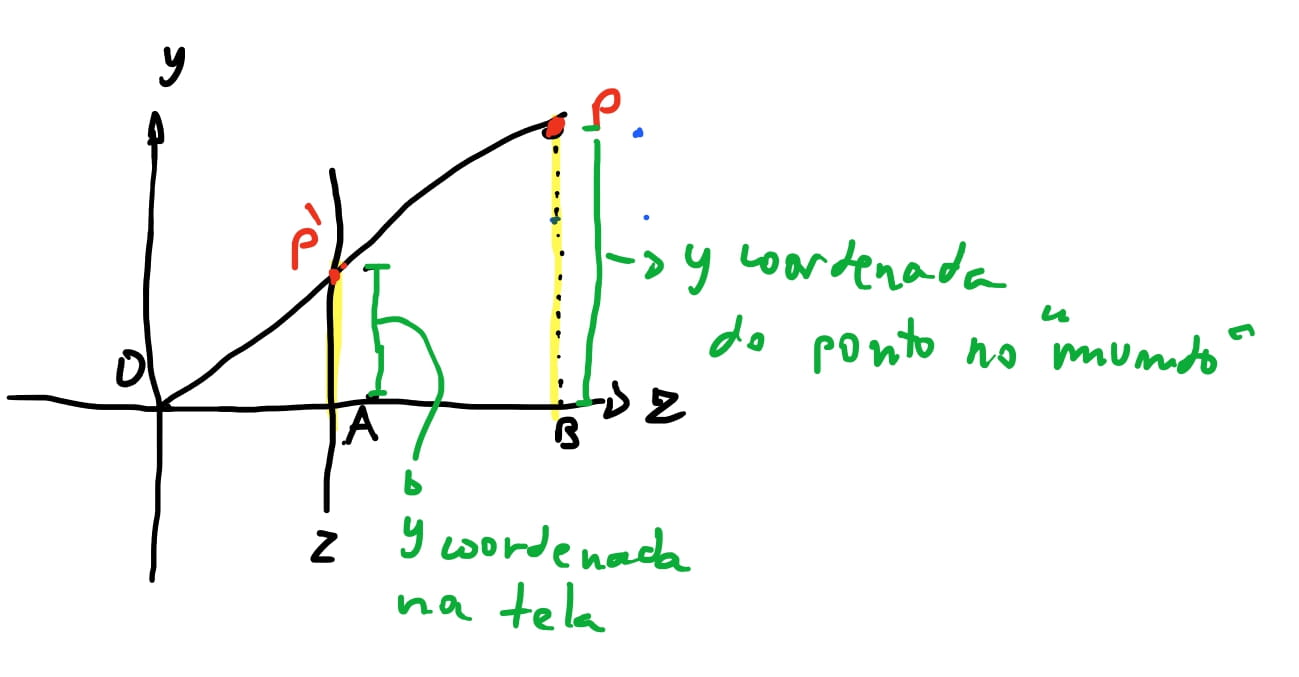
🤔 se queremos calcular o ponto \(P'\), podemos ver que o valor da sua \(y\)-coordenada é o segmento \(\overline{P'A}\)(para ser mais correto: é o valor do segmento \(\overline{P'A}\) projetado no eixo \(y\)).Sabemos também que o valor da sua \(z\)-coordenada é a mesma da distancia plano \(proj\) da origem. Se usarmos a proporção do triangulo de que \(\frac{\overline{P'A}}{\overline{OA}} = \frac{\overline{PB}}{\overline{OB}}\) então podemos chegar que \(\overline{P'A} = \frac{\overline{OA} * \overline{PB}}{OP}\).

E sabemos todos os valores que vamos precisar nessa equação: \(\overline{PB}\) é o valor da \(y\)-coordenada do ponto \(P\). O valor \(\overline{OA}\) é a distancia do plano de projeção da nossa origem no eixo \(z\), portanto, \(d\). E por fim o valor de \(\overline{OB}\) é a \(z\)-coordenada do ponto \(P\). Então temos:

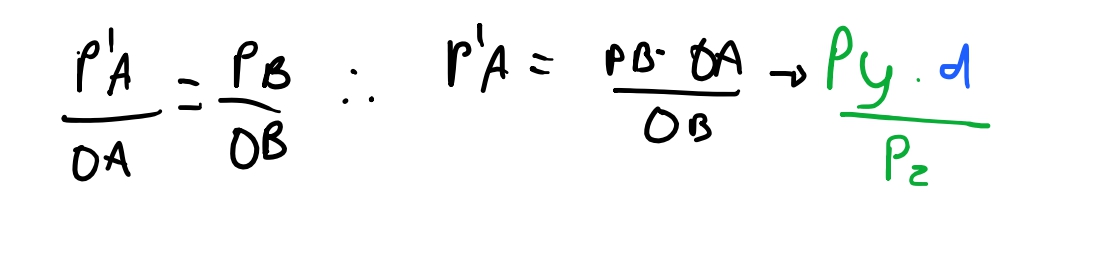
Para o eixo \(x\) vamos ter a reciproca! Só que dessa vez vamos olhar como se olhássemos a nossa cena de cima. Com o eixo \(z\) para cima, o eixo \(x\) para os lados e o eixo \(y\) como se tivesse apontado para nós.

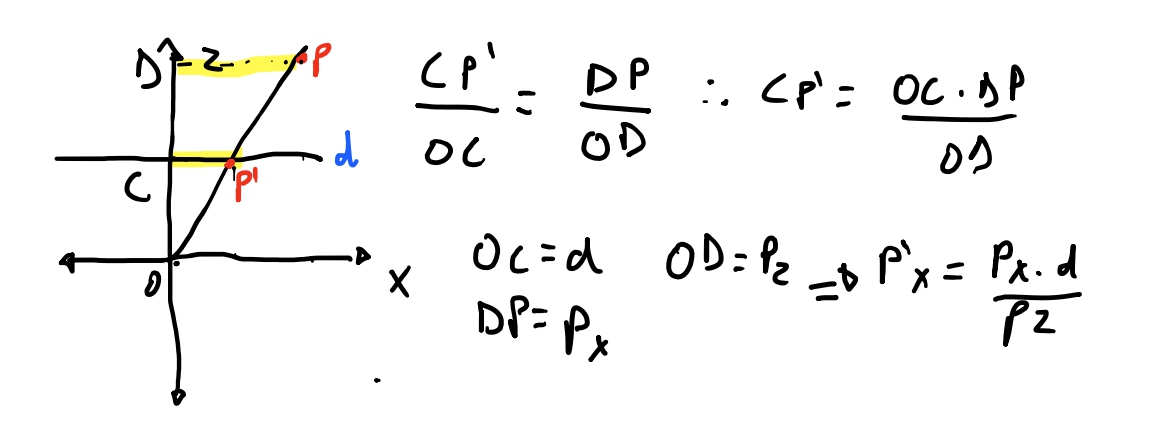
Chegamos em uma equação bem similar, porem considerando a \(x\) coordenada. Agora sabemos encontrar a posição de um ponto qualquer no mundo projetado no nosso plano de projeção. Vamos testar para ver se acontece como planejado!

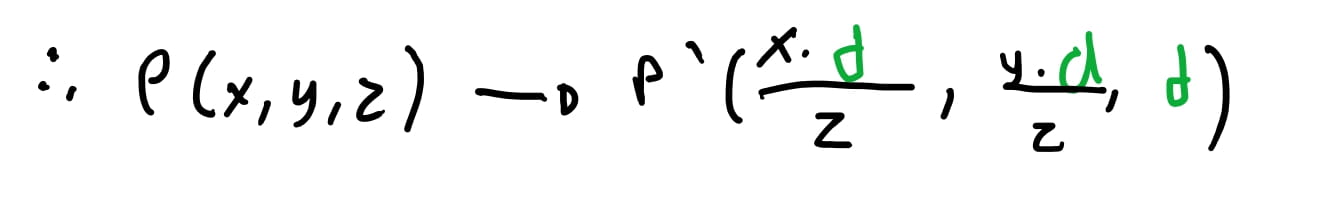
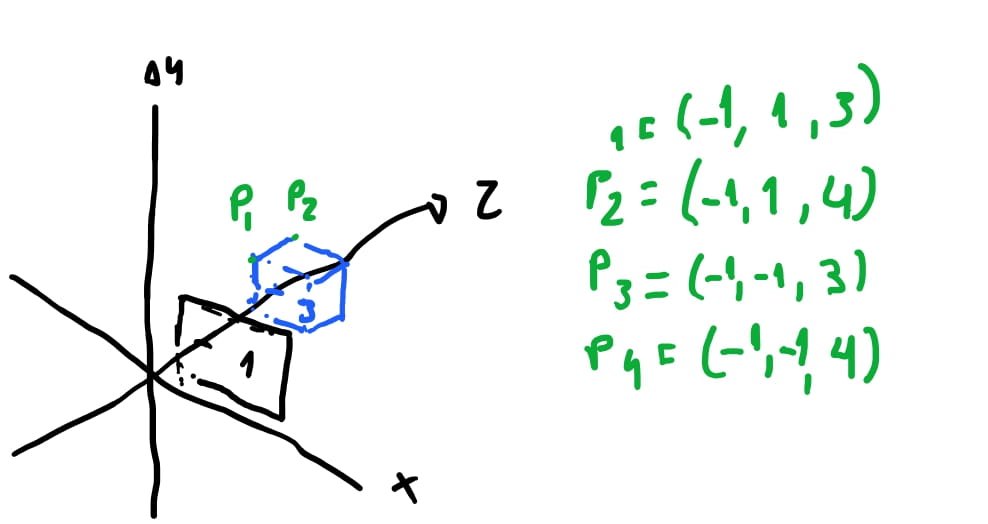
Vamos supor que nosso plano de projeção esteja a uma distancia de \(d = 1\) do eixo \(z\). Isto é, imagine que o centro do plano esteja em \(proj = (0,0,1)\). E imagine que temos um cubo que tenha os oito pontos à duas unidades na frente do nosso plano e tenha alguns dos pontos: \(P_1(-1, 1, 3)\),\(P_2(-1, 1, 4)\), \(P_3(-1, -1, 3)\), \(P_4(-1, -1, 4)\), \(...\).

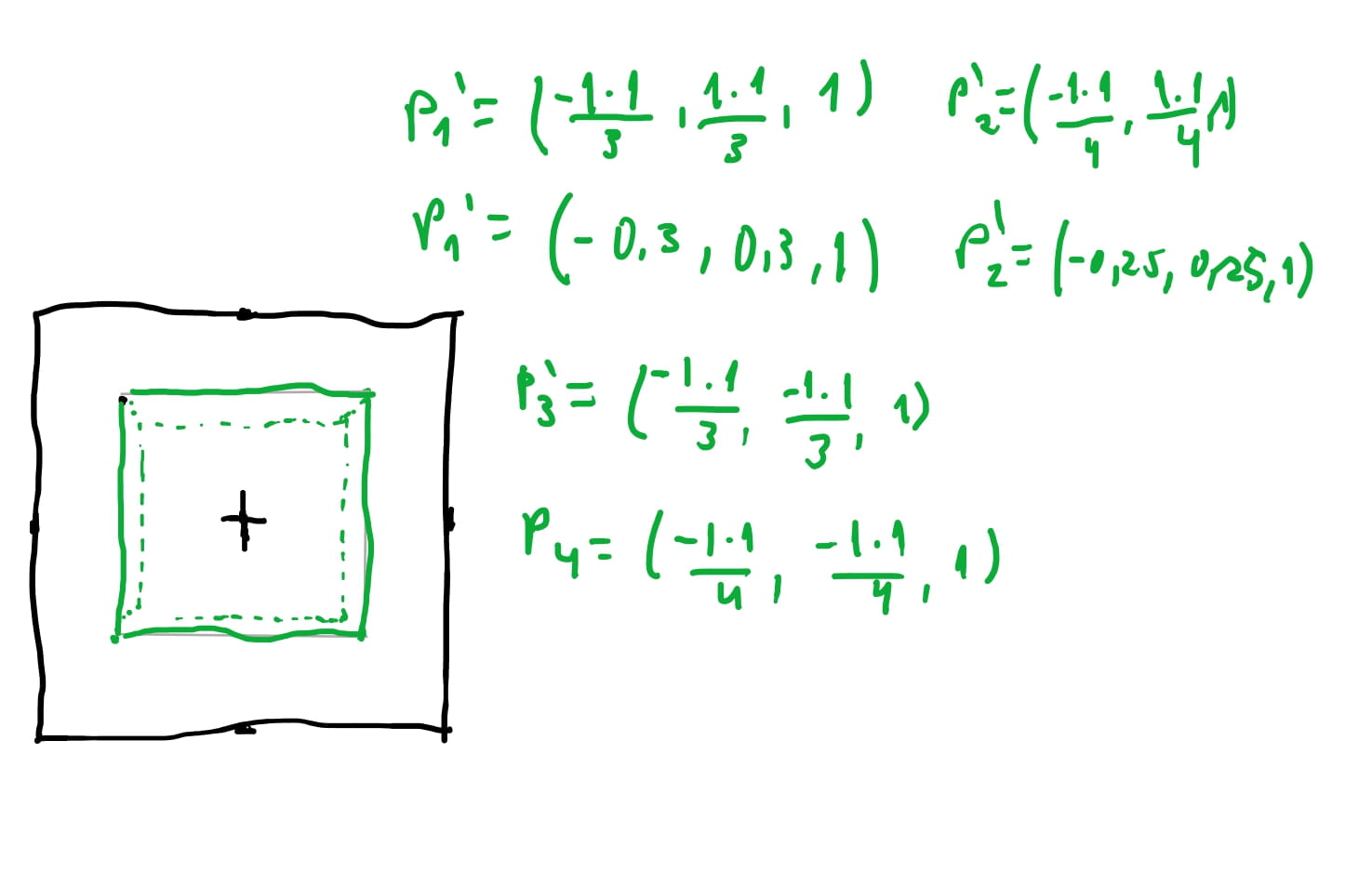
Se acompanhar as contas acima e desenhar os pontos que encontramos, os pontos que estiverem dentro do intervalo de nosso plano de projeção \([-0.5, 0.5]\) vão ser desenhados. E podemos conferir, como desenhamos à esquerda, que nosso algoritmo funciona! Podemos conferir que \(P_1(-1, 1, 3) => (-0.3, 0.3, 1)\). Uma percepção da nossa visão é que realmente quanto mais longe as coisas estão de nós, menor elas parecem ficar. Então faz sentido os nossos cálculos dividir por \(z\) ou seja a distancia da origem que o objeto está do observador, menor parece ficar … o tamanho aparente é inversamente proporcional à distancia do observador 😅.

hora de implementar !

Então agora que temos as equações nas mãos e vemos que funciona, é hora de transformar em código. Então o que queremos fazer é descrever a nossa cena, colocando onde está nosso plano de projeção, e o nosso cubo. Vamos então mapear os pontos da nossa cena, para as coordenadas do plano. Com essas coordenadas no nosso plano, vamos mapear elas para os pixels da tela e por fim, desenhar as linhas entre cada ponto. Devemos perceber então que as linhas são desenhadas na tela, e não no “plano de projeção”.

plano_projeção:
  | distancia => d
  | largura, altura => plano_largura, plano_altura

cubo:
  | vértice1 = (x:-1, y:1, z:3)
  | vértice2 = (x:1, y:1, z:3)
  | vértice3 = (x:-1, y:-1, z:3)
  | vértice4 = (x:1, y:-1, z:3)

  | vértice5 = (x:-1, y:1, z:4)
  | vértice6 = (x:1, y:1, z:4)
  | vértice7 = (x:-1, y:-1, z:4)
  | vértice8 = (x:1, y:-1, z:4)

função map_projeção->tela (x, y, z):
  retorne {
    x : x * (largura_da_tela / plano_largura),
    y: y * (altura_da_tela / plano_altura)
  }

função projetar_ponto(x, y, z):
  return {
    x: (x * d) / z,
    y: (y * d) / z,
  }

Com essas funções e os vértices do cubo, agora basta que liguemos cada cubo, desenhando as arestas dos cubos chamando a função de desenhar_linha que vimos no post anterior. Então vamos ligar cada aresta manualmente:

// p1 -> p2
desenhe_linha(
  map_projeção->tela(
    projetar_ponto(vértice1)
  ),
  map_projeção->tela(
    projetar_ponto(vértice2)
  )
)
// p2->p3
desenhe_linha(
  map_projeção->tela(
    projetar_ponto(vértice2)
  ),
  map_projeção->tela(
    projetar_ponto(vértice3)
  )
)
// p3->p4
desenhe_linha(
  map_projeção->tela(
    projetar_ponto(vértice3)
  ),
  map_projeção->tela(
    projetar_ponto(vértice4)
  )
)
// p4->p1
desenhe_linha(
  map_projeção->tela(
    projetar_ponto(vértice4)
  ),
  map_projeção->tela(
    projetar_ponto(vértice1)
  )
)
...
// desenhe linhas entre as arestas do cubo

E assim faremos para todas as arestas.

Por fim temos a seguinte imagem:

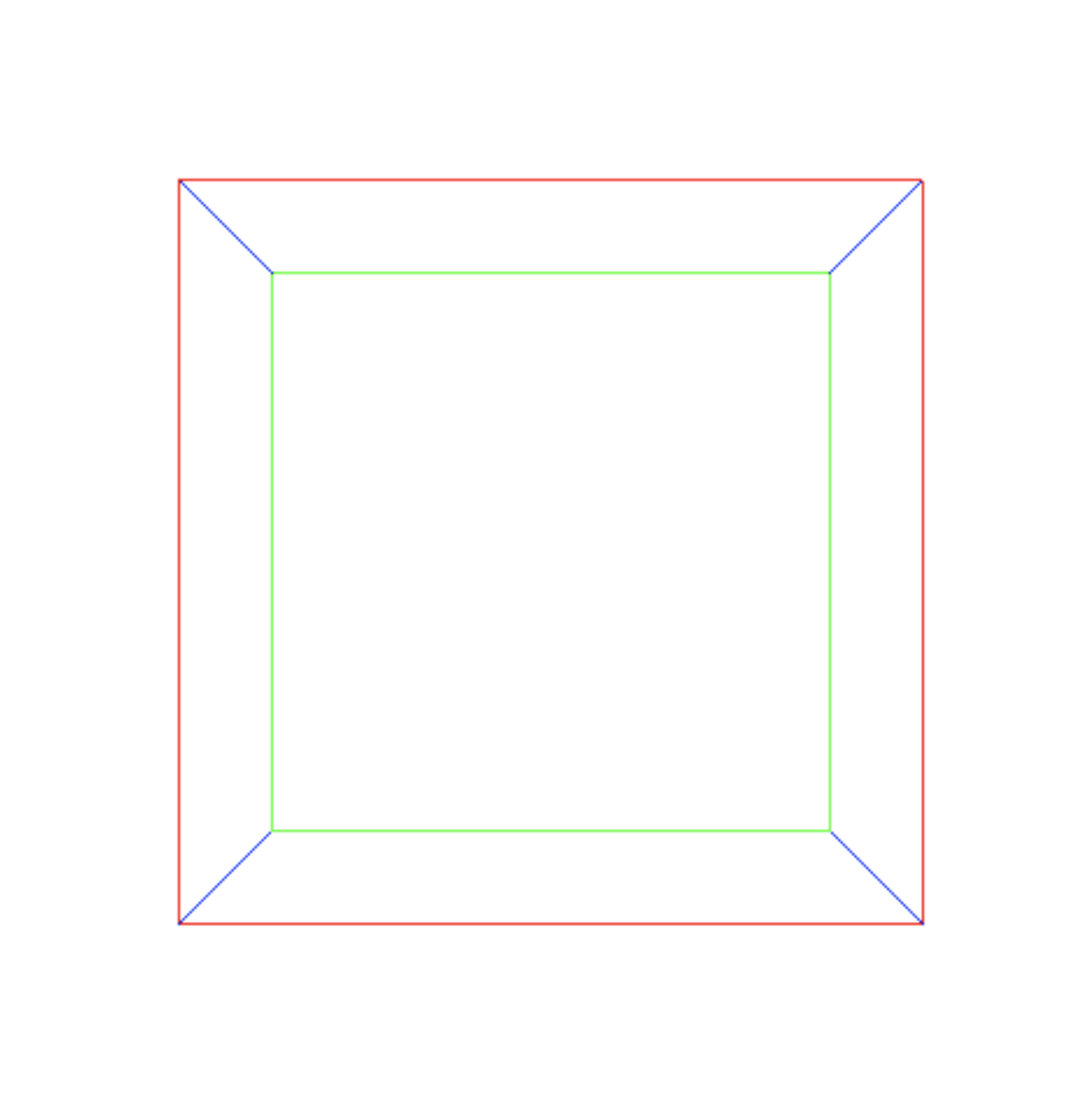
segue a nossa implementação

const canvas = document.getElementById("canvas");
const context = canvas.getContext("2d");

const width = canvas.width;
const height = canvas.height;

const canvasBuffer = context.getImageData(0, 0, width, height);

const blit = () => {
  context.putImageData(canvasBuffer, 0, 0);
};

const canvasPixel = (x, y, r, g, b, a) => {
  x = Math.floor(x);
  y = Math.floor(y);
  const index = (x + y * width) * 4;
  canvasBuffer.data[index + 0] = r;
  canvasBuffer.data[index + 1] = g;
  canvasBuffer.data[index + 2] = b;
  canvasBuffer.data[index + 3] = a;
};

const putPixel = (x, y, color) => {
  let canvasX = width / 2 + x;
  let canvasY = height / 2 - y;

  canvasPixel(canvasX, canvasY, color.r, color.g, color.b, color.a);
};

const drawLine = (p0, p1, color) => {
  let dx = p1.x - p0.x;
  let dy = p1.y - p0.y;

  if (Math.abs(dx) > Math.abs(dy)) {
    if (p0.x > p1.x) {
      let copy = p1;
      p1 = p0;
      p0 = copy;
    }
    const a = dy / dx;
    let b = p0.y - a * p0.x;

    for (let x = p0.x; x < p1.x; x++) {
      let y = a * x + b;
      putPixel(x, y, color);
    }
  } else {
    if (p0.y > p1.y) {
      let copy = p1;
      p1 = p0;
      p0 = copy;
    }

    const a = dx / dy;
    const b = p0.x - a * p0.y;

    for (let y = p0.y; y < p1.y; y++) {
      let x = a * y + b;
      putPixel(x, y, color);
      // x = x + a;
    }
  }
};

const RED = { r: 255, g: 0, b: 0, a: 255 };
const BLUE = { r: 0, g: 0, b: 255, a: 255 };
const GREEN = { r: 0, g: 255, b: 0, a: 255 };

let vP1 = { x: -1, y: 1, z: 3 }
let vP2 = { x: 1, y: 1, z: 3 }
let vP3 = { x: -1, y: -1, z: 3 }
let vP4 = { x: 1, y: -1, z: 3 }

let vP5 = { x: -1, y: 1, z: 4 }
let vP6 = { x: 1, y: 1, z: 4 }
let vP7 = { x: -1, y: -1, z: 4 }
let vP8 = { x: 1, y: -1, z: 4 }


const PLANE_DISTANCE = 1;
let projectVertex = (vertex) => {
  return { x: (vertex.x * PLANE_DISTANCE) / vertex.z, y: (vertex.y * PLANE_DISTANCE) / vertex.z, z: vertex.z }
}

const PLANE_WIDTH = 1;
const PLANE_HEIGHT = 1;
const viewPortToCanvas = ({ x, y, z }) => {
  return { x: x * (width / PLANE_WIDTH), y: y * (height / PLANE_HEIGHT) }
}

drawLine(viewPortToCanvas(projectVertex(vP1)), viewPortToCanvas(projectVertex(vP2)), RED)
drawLine(viewPortToCanvas(projectVertex(vP2)), viewPortToCanvas(projectVertex(vP3)), RED)
drawLine(viewPortToCanvas(projectVertex(vP3)), viewPortToCanvas(projectVertex(vP4)), RED)
drawLine(viewPortToCanvas(projectVertex(vP4)), viewPortToCanvas(projectVertex(vP1)), RED)

drawLine(viewPortToCanvas(projectVertex(vP5)), viewPortToCanvas(projectVertex(vP6)), GREEN)
drawLine(viewPortToCanvas(projectVertex(vP6)), viewPortToCanvas(projectVertex(vP7)), GREEN)
drawLine(viewPortToCanvas(projectVertex(vP7)), viewPortToCanvas(projectVertex(vP8)), GREEN)
drawLine(viewPortToCanvas(projectVertex(vP8)), viewPortToCanvas(projectVertex(vP4)), GREEN)

drawLine(viewPortToCanvas(projectVertex(vP1)), viewPortToCanvas(projectVertex(vP5)), BLUE)
drawLine(viewPortToCanvas(projectVertex(vP2)), viewPortToCanvas(projectVertex(vP6)), BLUE)
drawLine(viewPortToCanvas(projectVertex(vP3)), viewPortToCanvas(projectVertex(vP7)), BLUE)
drawLine(viewPortToCanvas(projectVertex(vP4)), viewPortToCanvas(projectVertex(vP8)), BLUE)

blit();

o que escondemos ?

Acabamos não falando de angulo de visão ou porque desenhamos as linhas em alguma ordem específica. O tamanho e a posição do plano vai dizer qual angulo de visão a câmera terá.Até agora apenas esbarramos na superfície da computação gráfica, mas já temos uma boa ideia de como a matemática da projeção funciona. E isso vai nos dar alguma liberdade para nos próximos textos pensarmos apenas como podemos estender este exemplo para gráficos mais abrangentes. Vamos falar de como podemos criar objetos tridimensionais quaisquer e movimenta-los pelo mundo tridimensional.

Agora que temos ambos esquadro e caneta, Urizen vai poder criar seu mundo de razão. Nos poemas de Blake, Urizen, ou a razão humana, vagueia por ai dando nomes e dividindo as coisas para entende-las. E esse é apenas o nosso começo do poema. Em um ponto do poema, Urizen se encontra acorrentado pelas correntes de Los, o principio criativo da mente humana. Somente então Los cria uma imagem humana de Urizen, e a união perfeita do homem com a sua Razão (Urizen) e sua Imaginação (Los) cria o homem perfeito Albion. Até chegar-mos ao fim de um rasterizador completo e finalmente Urizen ver a si isolado no seu próprio mundo vazio e acorrentado pela própria criação é que daremos espaço para Los nascer e conseguiremos deixar com que a nossa criatividade embelezar nosso mundo tridimensional de árvores, arte e musica. Mas não se deixem enganar: ainda é um mundo artificial de Urizen!