Decidi escrever este texto em português porque pensei: “hmmm.. acho que ja existe material mais que suficiente em ingles, mas para o publico brasileiro existe pouco material” e eu pensei no pequeno eu com 12 anos que queria entender como computação gráfica funcionava e não tinha acesso nem a livros bem escritos quanto compreensão de ingles o suficiente. Então pensando nisso, decidi escrever em português
O que você deve esperar?
Daqui em diante eu quero te levar em uma sequencia de textos para desmistificar algumas ideias de matemática e computação. A ideia é te mostrar que tudo pode ser mais simples. Eu vou mostrar os cálculos e como chegar neles e acho que essa forma de “abrir” e “levantar os véus” Apokalipsis é o melhor jeito de aprender sobre um assunto. O texto irá da ideia simples de como desenhar um pixel na tela, e seguiremos a sequencia de: como desenhar uma linha, como desenhar um triangulo, como preencher este triangulo, como desenhar uma figura tridimensional projetada em uma superfície bidimensional, e preencher com o mesmo algoritmo de triângulos, como colocar perspectiva nos triângulos que iremos desenhar. Com isto tudo em mente nos próximos textos vamos abortar as bibliotecas gráficas que conversam com a placa de video e fazem tudo isso para o desenvolvedor e de forma rápida.
O que voce precisa saber?
Gostaria que ninguém precisasse saber nada. Não precisa perfeitamente confortável com matemática, mas caso não seja o caso, eu peço que acompanhe genuinamente os cálculos e vou explicar o mais sucintamente que puder e talvez voce possa desenvolver certa facilidade. Não é nada extraordinariamente mais avançado do que uma aula de matemática normal, apenas sendo “aplicado”.
What about english?
Yea, my previous text were in english, and I plan to translate this one to english too, so wait for it, or … google translate this one. But .. there is already plenty material, which will be quoted at the end of this text so you can have some sources of your own.
Começando do começo: como desenhar uma linha ?
“Dê-me uma alavanca e um ponto de apoio e eu moverei o mundo” essa frase de Arquimedes poderia ser facilmente aplicada para a computação gráfica: “Dê-me uma função de desenhar retas e eu irei desenhar qualquer forma”. A ideia por trás disso é que se pudermos desenhar livremente linhas com o controle fino que quisermos, podemos decompor qualquer figura em desenho de linhas. Então espero ter justificado o porque dos próximos parágrafos e com esse argumento espero que acompanhe sem muita reclamação e tédio os próximos parágrafos que estão vindo.
um pouquinho de matematica
Vamos imaginar que queremos desenhar uma reta no plano entre dois pontos.
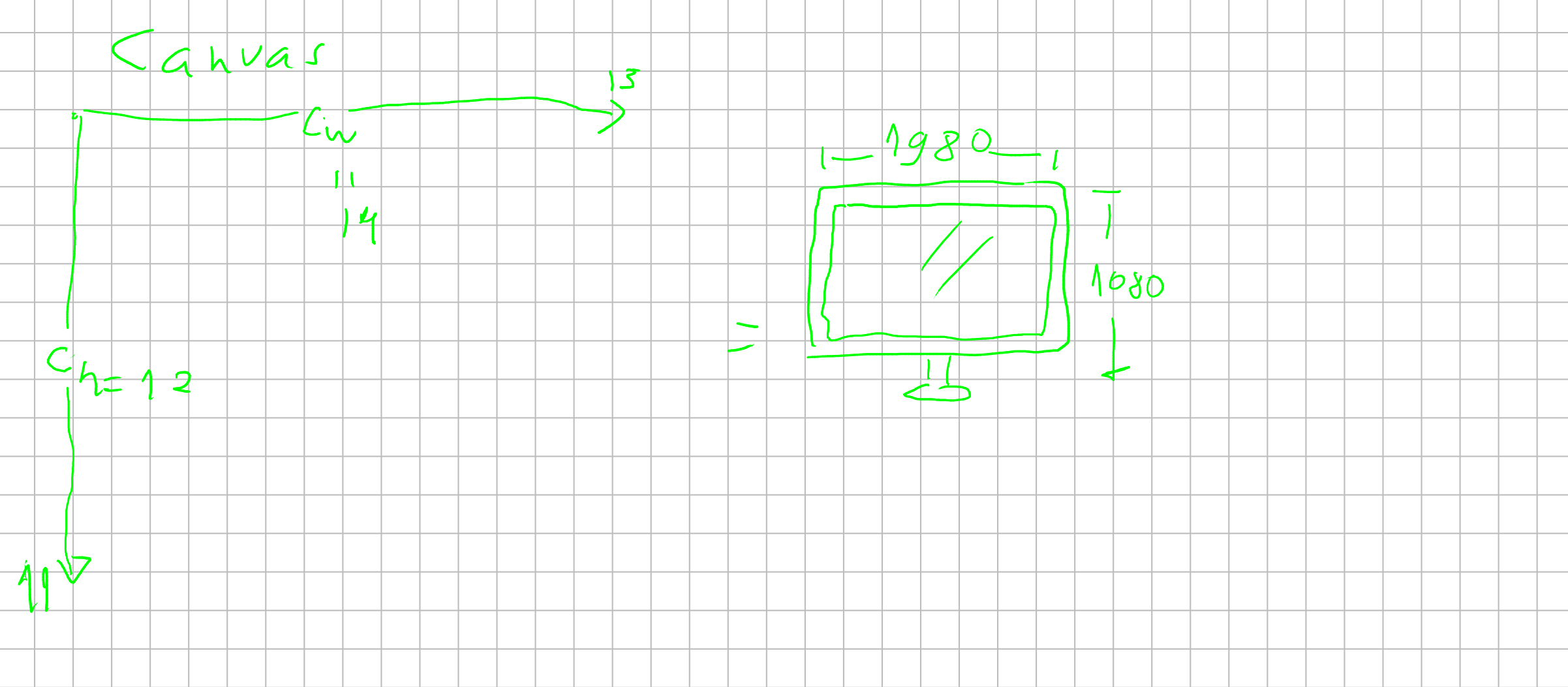A tela de um computador (como vista no texto de raytracing) é representada como a imagem acima: (eixo \(x\) cresce para direita, e o eixo \(y\) cresce para baixo.
Então vamos imaginar como vamos desenhar um ponto na tela usando este tipo de coordenada
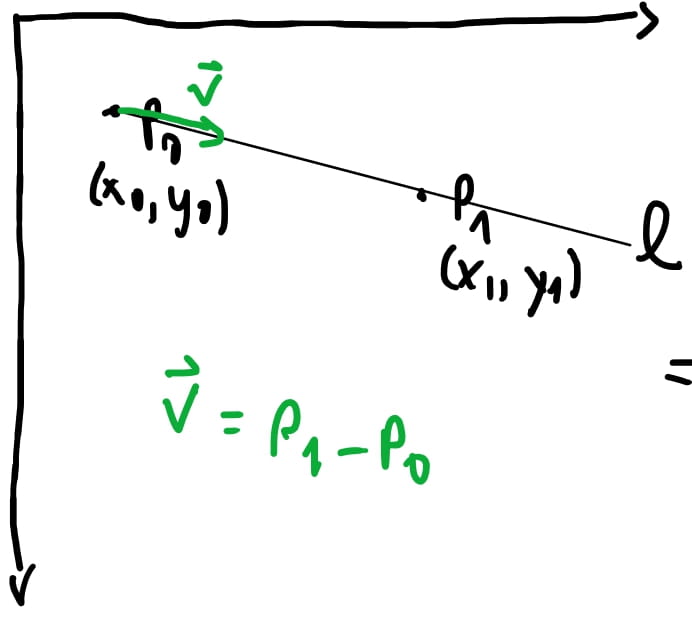
Então como na imagem acima temos \(P_0\) e queremos desenhar uma linha até \(P_1\). Podemos pensar que podemos pegar qual a direção para o \(P_1\) à partir de \(P_0\) e pintar cada pixel naquela direção e então, fazemos isso até chegar em \(P_1\).
Representando esta ideia matematicamente queremos dizer que um ponto \(P\) na reta entre \(P_0\) e \(P_1\) vai ser igual à \(P = P_0 + \vec{v} * t\) onde \(t\) vai ser um numero qualquer. Ou seja, se \(t = 0\), \(P\) vai ser igual a \(P_0\). Se \(t=1\), então \(P\) vai ser igual \(P_1\). Então modelamos uma equação que modela essa reta entre os dois pontos porem \(t\) tem que estar entre \(0 e 1\).
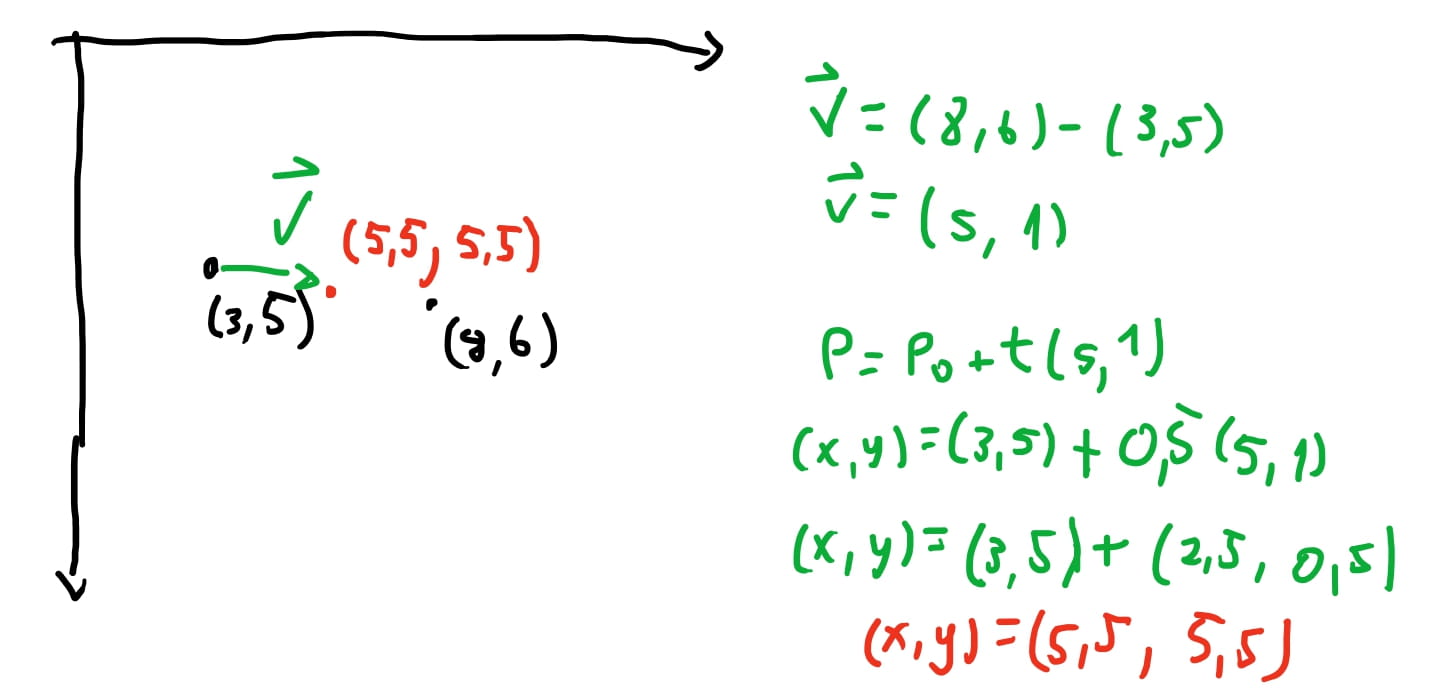Na imagem acima vemos um exemplo de como usamos esta equação que modelamos para encontrar um ponto na reta. Fizemos \(t = 0.5\) e encontramos um ponto na reta \(l\) em que \(P = (5.5, 5.5)\).
Porem como podemos fazer para encontrar os pixels na tela? Vamos lembrar que o pixel é “discreto”. Quando digo “discreto” digo que é um valor “inteiro”, ou seja, o pixel \((5.5, 5.5)\) não existe na tela, apenas o pixel \((5,5)\). Então se fizéssemos uma função como iterar entre 0 e 1 e incrementar \(0.01\), Iteraríamos mil vezes e repetiríamos muitos valores: Todos valores entre \(5.001\) e \(5.599\) seriam o mesmo pixel. Talvez não pareça tão ruim agora mas imagine que vamos usar esta mesma função para preencher triângulos e no futuro cada polígono tridimensional vai ter milhares de triângulos, então ja imagine o quanto essa função vai fazer o computador trabalhar atoa.
OBS: Se você é um programador de primeira viagem, recomendo a leitura do texto Why early optimization is the root of all evil em que o autor alerta sobre optimização prematura do código. O que estamos fazendo aqui pode ser um exemplo de optimização prematura ja que antes mesmo de acontecer o problema de custo computacional ja estamos corrigindo ele. Porem, estou me atendo a este ponto agora pois acho didático lidar com a ideia do algoritmo de desenho de linhas e deixar este problema fora de vista para os problemas que virão futuramente!
Então vamos tentar melhorar nossa equação. Queremos saber apenas os pontos que estão na reta ( o que nossa equação atualmente ja nos oferece), porem, queremos apenas as coordenadas “discretas”. E além disso, queremos fazer o mínimo de iterações possíveis. De preferencia, pra cada valor de \(x\) a equação retorne um valor de \(y\) ou vice-versa. Como podemos fazer isso ??
Então vamos estender um pouco nossa equação. Sabemos que \(P = (x,y)\), ou seja, um ponto é um conjunto de coordenadas no plano \(x,y\).
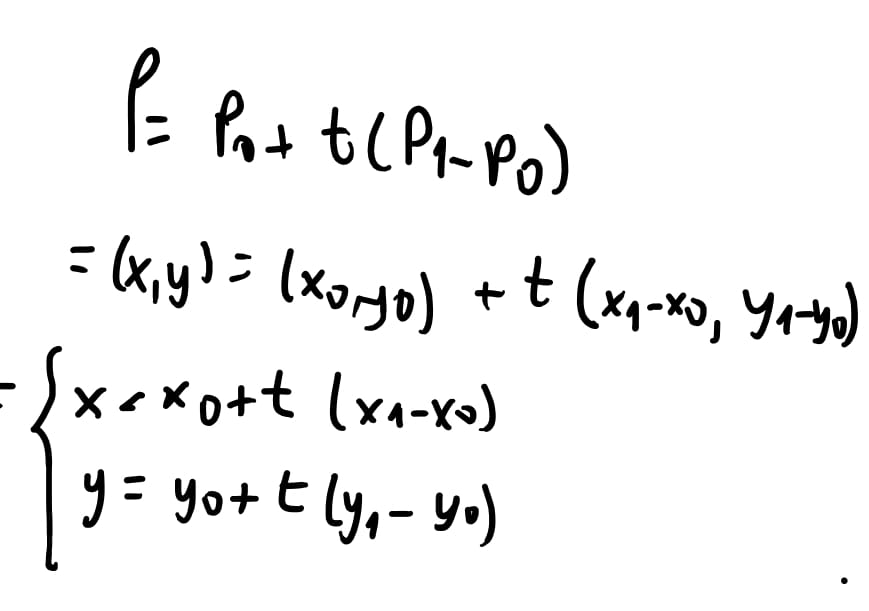Decompomos então a nossa equação em \((x,y) = (x_0, y_0) + t * ( x_1 - x_0 , y_1 - y_0)\). O motivo dessa subtração é que para encontrar a direção de um ponto para o outro (chamamos essa direção de vetor) fazemos \(ponto Final - ponto Inicial\) e isto nos dá o “vetor” que aponta do ponto inicial para o ponto final.
E então, com a nossa equação decomposta em \((x,y)\), vamos separar por variável e separáramos em um sistema de equações. \(x = x_0 + t (x_1 - x_0)\) e similar para \(y\). Vamos isolar então a única variável em comum às duas equações \(t\). E então vamos substituir o que encontrar-mos como valor de \(t\) na segunda equação. Assim vamos chegar em apenas uma equação com as duas variáveis. Lembrando que o nosso objetivo é chegar em uma equação que nos dê o valor de \(y\) para cada \(x\).
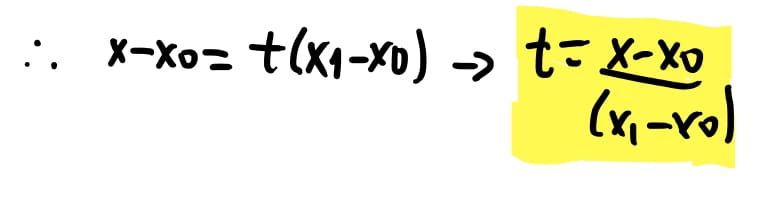Isolando o \(t\) encontramos que \(t = \dfrac{x - x_0}{x_1 - x_0}\)
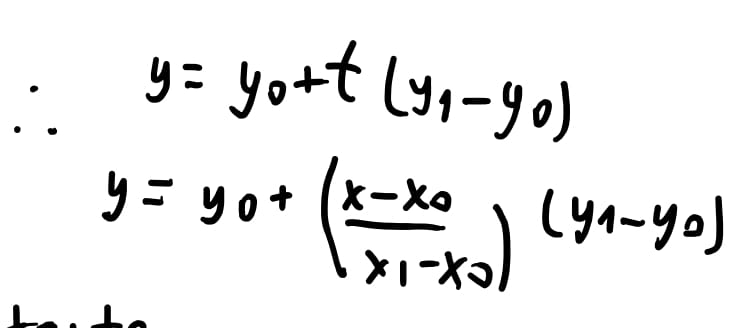Fazendo a substituição do nosso valor de \(t\) na equação de \(y\) encontramos que \(y = y_0 + \dfrac{x-x_0}{x_1 - x_0} * (y_1 - y_0)\).
Mas como sabemos que iniciamos em \(P_0\) e vamos para \(P_1\), então significa que temos os valores de ambos os pontos. Então vamos chamar \(\dfrac{y_1 - y_0}{x_1 - x_0}\) de \(a\) porque sabemos que o valor desta divisão é constante. Ou seja, assim que definimos os dois pontos, sabemos qual o valor de \(a\). No nosso exemplo la de cima, em que \(P_0 = (3,5)\) e \(P_1 = (8,6)\), teríamos que \(a = \dfrac{6-5} {8-3} = \dfrac{1}{5}\).
Percebemos também que se fizermos a multiplicação de \(a\) por \((x-x_0)\) restante, encontramos outras constantes: \(y_0\) e \(-a * x_0\). Que vamos chamar de \(b\).
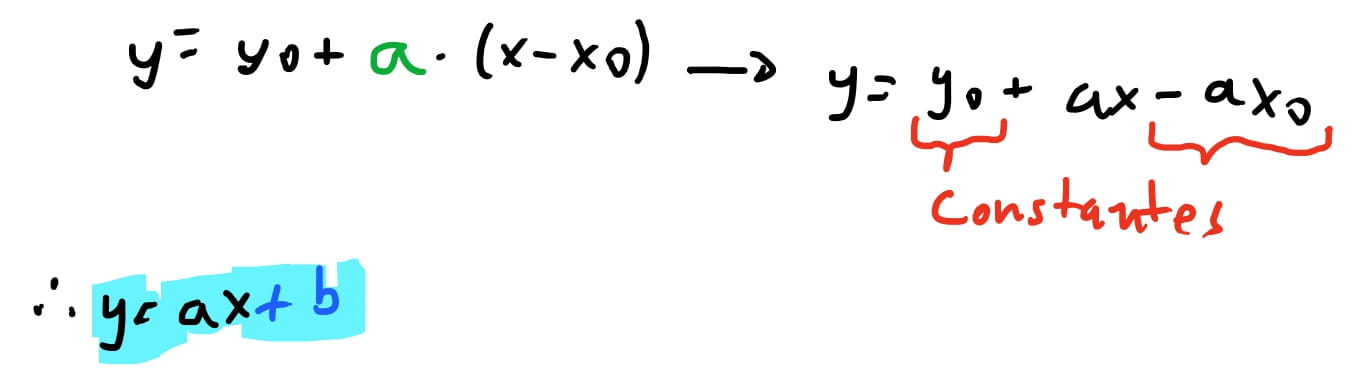Resultando na equação de reta. Nesta equação conseguimos obter um valor de \(y\) para cada valor de \(x\) entrado.
Vamos para um exemplo
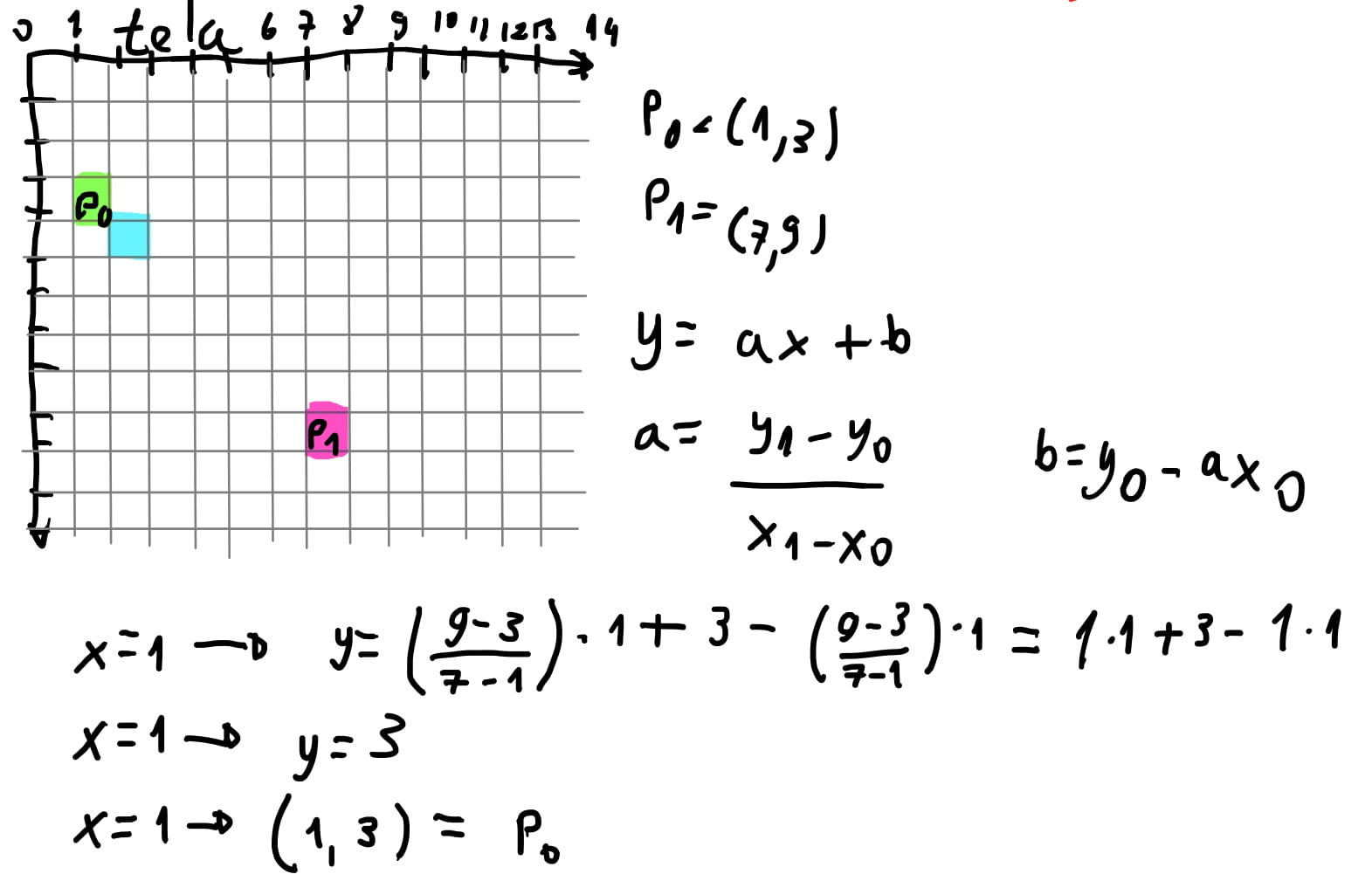Para \(x = 1\) constatamos que o \(y = 3\), ou seja, confirmamos a posição de \(P_0\).
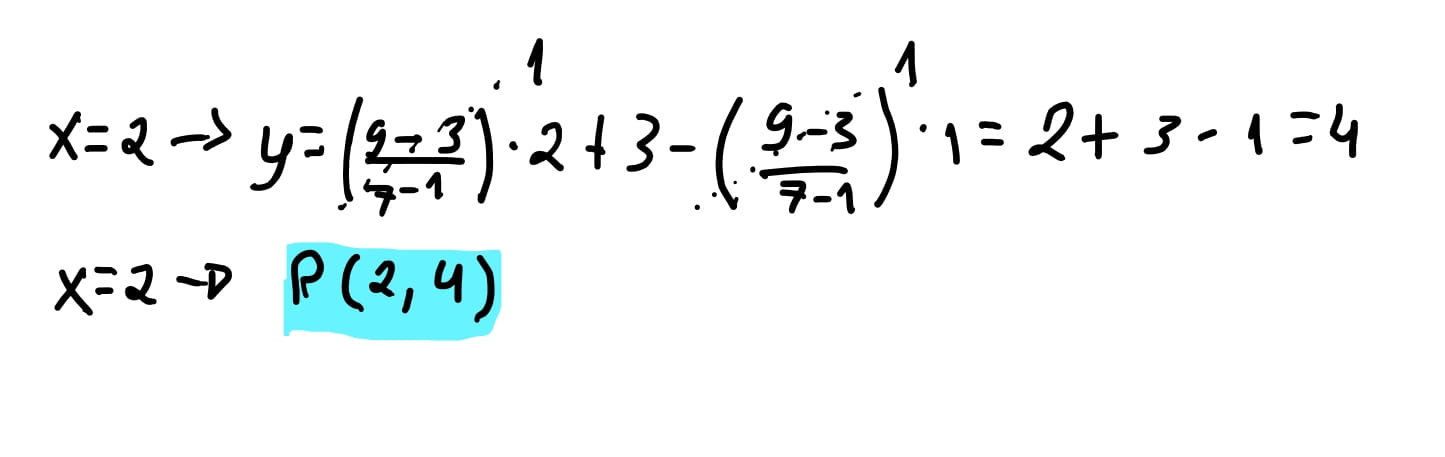
Então vamos escrever nosso pseudo código pra escrever linhas, lembrando que temos apenas uma função disponível da tela que é putPixel(x, y, color) como visto no post anterior.
function drawLine(p0, p1, color):
a = p1.y - p0.y / p1.x - p0.x
b = p0.y - a * p0.x
for x = p0.x ; x <= p1.x; x++:
y = a*x + b
putPixel(x, y, color)
No qual nossa função apenas recria o comportamento da função que encontramos e faz um laço entre \(x\) de \(P_0\) e \(x\) de \(P_1\).
Porem, ao implementarmos o código acima nos deparamos com os seguinte bug:
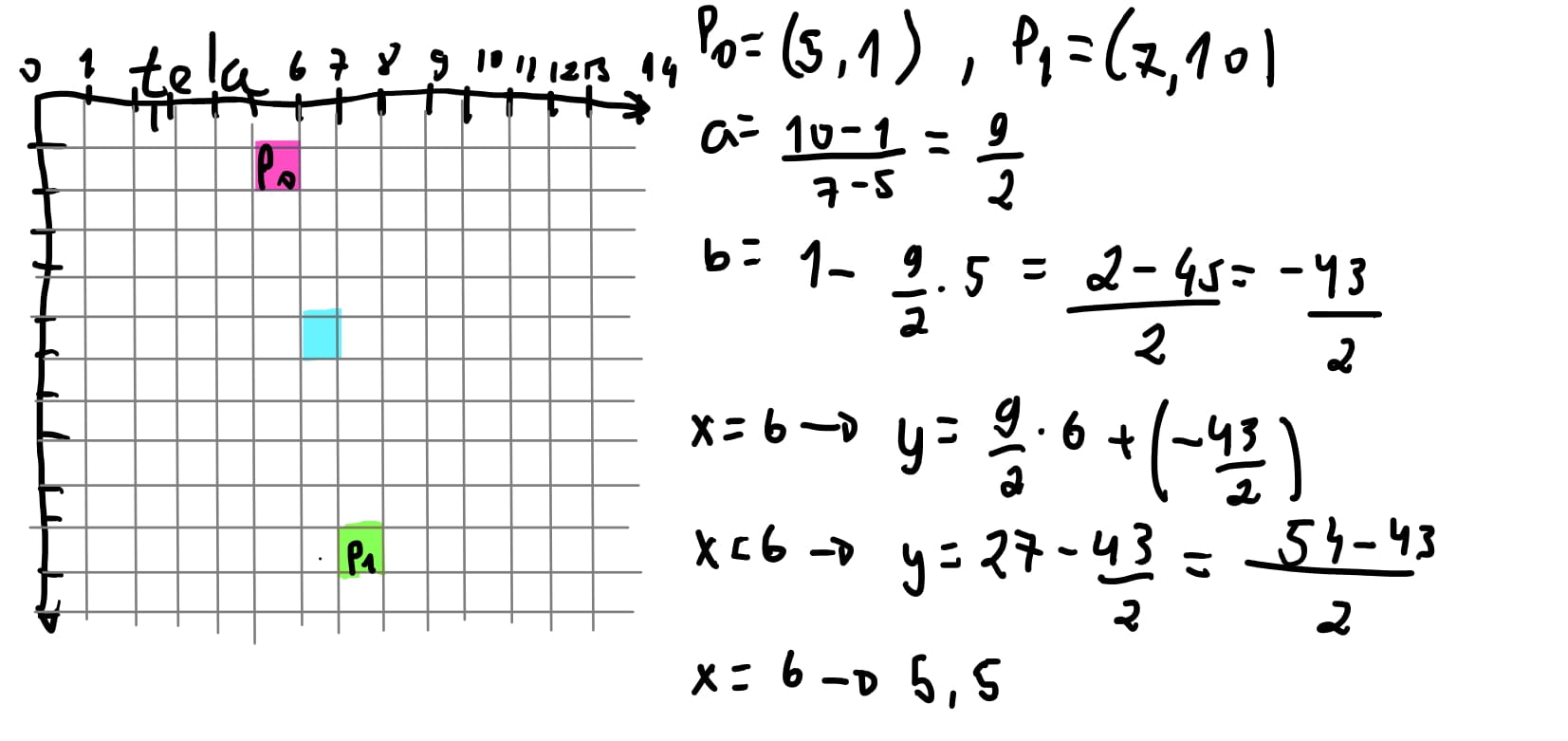Quanto mais inclinada é a reta, teremos, como no exemplo acima, apenas um valor de \(x\) para vários pixels no eixo \(y\). Se a reta for completamente vertical, ou seja, o valor da coordenada \(x\) do ponto inicial e final é o mesmo, simplesmente não há iteração e logo não há nenhum pixel para ser colorido.
Apesar de haver apenas um valor de \(x\) para calcular algum pixel entre os dois pontos, há uma distancia de \(y\) dos dois pontos.Sendo os pontos \(P_0 = (5,1)\) e \(P_1 = (7,10)\), haveriam 9 valores em \(y\) para encontrarmos valores de \(x\). Poderíamos então procurar valores de \(x\) para cada valor de \(y\). Seria o inverso da função !
Vamos ver como faríamos isso!
Então imagine que “rotacionamos” a tela, e considere que trocamos os eixos \(x\) e \(y\). Poderíamos calcular qual valor de \(y\) para uma coordenada do pixel \(x\) dos pontos “invertidos”, sendo \(P_0 = (1, 5)\) e \(P_1 = (10,7)\). E usaríamos a mesma equação.
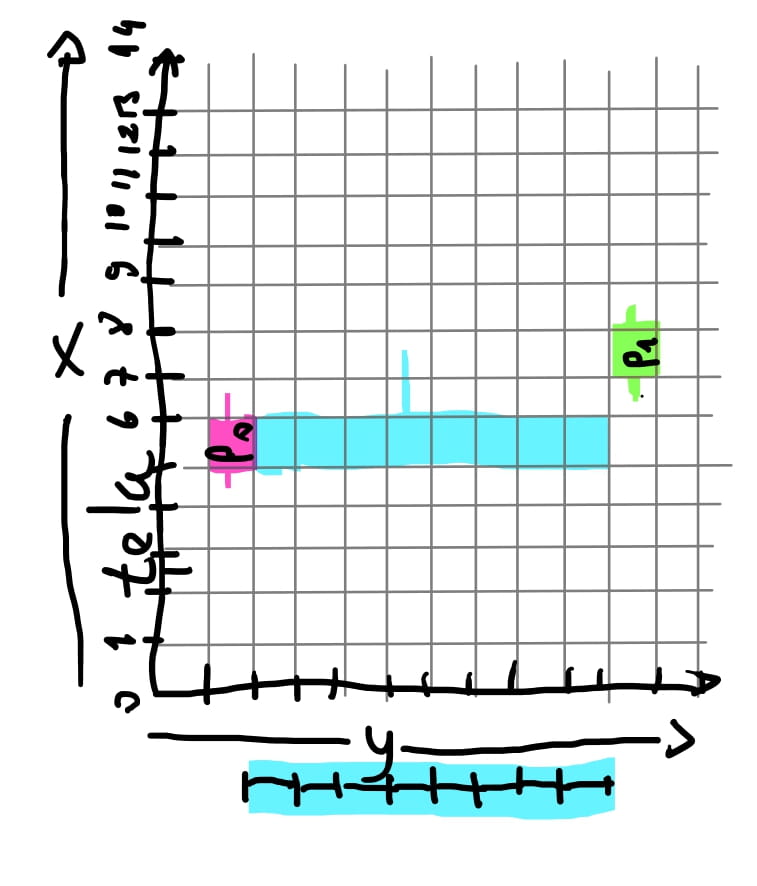
Agora que conseguimos encontrar uma equação independente da inclinação da reta, precisamos de um critério de quando vamos usar uma ou outra.
Podemos fazer um exercício mental: Imaginemos o angulo da reta (formador pelos pontos \(P_0\) e \(P_1\)) e o eixo \(x\). Quando este angulo é \(0 °\), há o máximo de pixels na horizontal. E quando este angulo é \(90 °\) o numero pixels é nulo. Mas em \(90 °\) o numero de pixels em \(y\) é o máximo. Então podemos dividir pela metade, e de \(0 °\) até \(45 °\) usamos \(x\) e de \(45 °\) até \(90 °\) usamos \(y\).
Vamos testar nossa hipótese e implementar nosso pseudocódigo desenvolvido até agora!
Como vimos, precisamos saber apenas se há mais pixels para iterar ou pelo eixo \(y\) ou pelo eixo \(x\). Então ao invés de consultamos por ângulos, podemos consultar pela “diferença” de pixels. O eixo que possuir mais pixels para iterar-mos será o eixo escolhido. Podemos pensar que nosso angulo é a “razão” do quanto um eixo aumenta em relação ao outro. Quanto maior o angulo, mais rápido \(y\) aumenta quando \(x\) aumenta.
function drawLine(p0, p1, color):
dx = abs(p1.x - p0.x)
dy = abs(p1.y - p0.y)
a = dy/dx
b = p0.y - a* p0.x
if dx > dy:
for x=p0.x; x<=p1.x; x++:
y = a*x + b
putPixel(x, y, color)
else:
for y=p0.y; y<=p1.y; y++:
x = (y-b)/a
putPixel(x, y, color)
O problema de usar \(\frac{y-b}{a}\) é que \(a\) vai ser uma divisão por zero quando a reta estiver “vertical”. Para isso vamos “inverter” a nossa equação em função de \(y\).
Estamos quase lá! Nosso algoritmo de linhas ainda tem um bug! Caso alguma coordenada de p0 seja menor que a coordenada de p1, não vamos conseguir iterar de um ponto ao outro. Então precisamos checar se isso é verdade, e caso seja, precisamos fazer um swap!
OBS: swap é um termo usado para trocarmos o valor de duas variáveis entre sí.
Caso p0 > p1 p0 = p1 e p1 = p0 e não vamos precisar alterar a lógica do nosso código. Vamos conseguir continuar usando os mesmos laços sem ter que fazer alguma iteração no sentido contrario.
function drawLine(p0, p1, color):
dx = abs(p1.x - p0.x)
dy = abs(p1.y - p0.y)
if dx > dy:
if p0.x > p1.x:
swap(p0, p1)
a = dy/dx
b = p0.y - a* p0.x
for x=p0.x; x<=p1.x; x++:
y = a*x + b
putPixel(x, y, color)
else:
if p0.y > p1.y:
swap(p0, p1)
// função linear "inversa"
a = dx/dy
b = p0.x - a* p0.y
for y=p0.y; y<=p1.y; y++:
x = a * y + b
putPixel(x, y, color)
Implementando o codigo!
Por fim temos nossa implementação do nosso algoritmo para desenhar linhas! Ainda podemos melhorar muito nosso algoritmo de linhas, existindo algoritmos mais poderosos para tal função como o algoritmo de Bresenham. Mas para o nosso fim, este algoritmo é bom o suficiente. Caso deseja, pode implementar o algoritmo de Bresenham que não mudará em nada o progresso daqui em diante.
const canvas = document.getElementById("canvas");
const context = canvas.getContext("2d");
const width = canvas.width;
const height = canvas.height;
const canvasBuffer = context.getImageData(0, 0, width, height);
const blit = () => {
context.putImageData(canvasBuffer, 0, 0);
};
const canvasPixel = (x, y, r, g, b, a) => {
x = Math.floor(x);
y = Math.floor(y);
const index = (x + y * width) * 4;
canvasBuffer.data[index + 0] = r;
canvasBuffer.data[index + 1] = g;
canvasBuffer.data[index + 2] = b;
canvasBuffer.data[index + 3] = a;
};
const putPixel = (x, y, color) => {
let canvasX = width / 2 + x;
let canvasY = height / 2 - y;
canvasPixel(canvasX, canvasY, color.r, color.g, color.b, color.a);
};
const drawLine = (p0, p1, color) => {
let dx = p1.x - p0.x;
let dy = p1.y - p0.y;
if (Math.abs(dx) > Math.abs(dy)) {
if (p0.x > p1.x) {
let copy = p1;
p1 = p0;
p0 = copy;
}
const a = dy / dx;
let y = p0.y;
for (let x = p0.x; x < p1.x; x++) {
putPixel(x, y, color);
console.log("x", x);
console.log("y", y);
y = y + a;
}
} else {
if (p0.y > p1.y) {
let copy = p1;
p1 = p0;
p0 = copy;
}
const a = dx / dy;
let x = p0.x;
for (let y = p0.y; y < p1.y; y++) {
putPixel(x, y, color);
x = x + a;
}
}
};
let initialPoint = { x: 10, y: -80 };
let finalPoint = { x: -110, y: 130 };
let redColor = { r: 255, g: 0, b: 0, a: 255 };
drawLine(initialPoint, finalPoint, redColor);
blit();
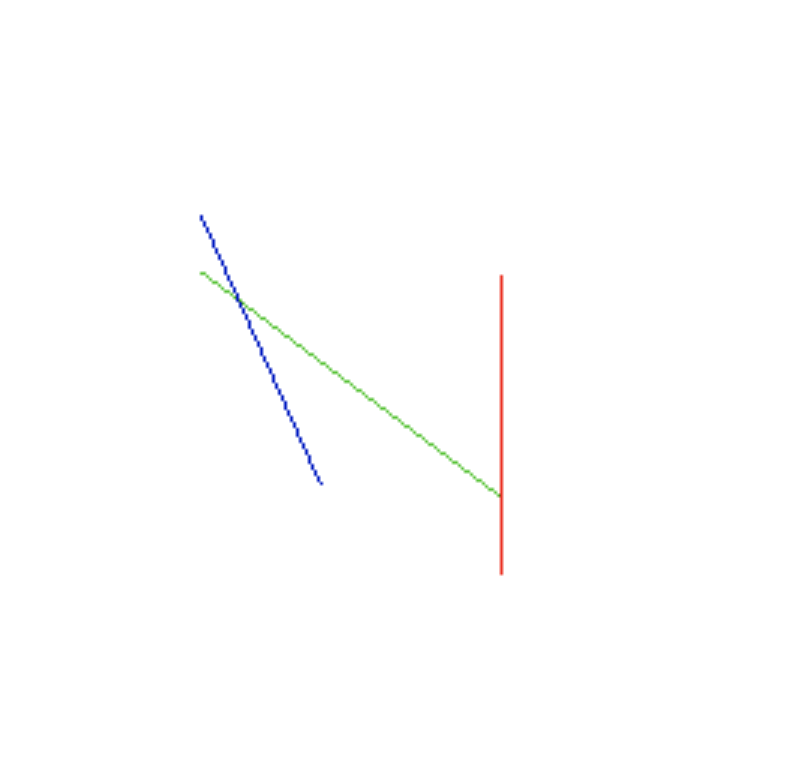
Veja o código funcionando em tempo real neste link
Até o proximo post!